Database : Normalization in Brief 📦 #
Introduction #
In this article, we are going to discuss about database normalization briefly. Database Normalization is a process, used to organize databases, introduced by Dr. Edgar F. Codd an IBM researcher. The concept was published in a paper titled A Relational Model of Data for Large Shared Data Banks in 1970. The main objective of database normalization is to organize relational databases into multiple smaller and related tables in such a way that,
- Eliminate unnecessary duplication (redundancy)
- Reduce the risk of data anomalies occurring during DB operations
- Make logical relationships between data more sound
- Improve data integrity (accuracy, consistency, reliability of Data)
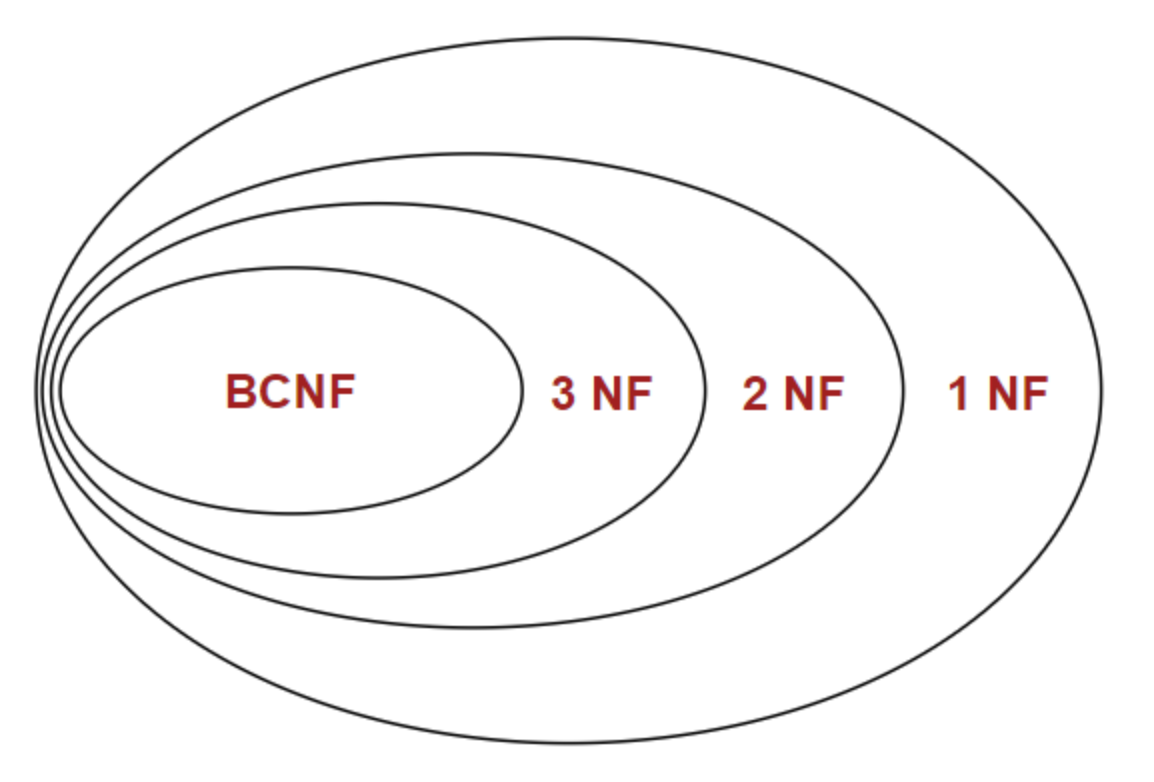
Levels of Normalization #
Here, we discuss the following levels of normalization.
- First Normal Form (1NF)
- Second Normal Form (2NF)
- Third Normal Form (3NF)
- Boyce–Codd Normal Form (BCNF)
Let’s discuss each one by one. Here I’ll try to explain using practical examples without going deep into theoretical aspects.
Note that X -> Y, simply means using X we can determine Y
First Normal Form #
In the first normalization form, we ensure that the values in each column are atomic, which means they cannot be further divided. The main aim of this is to avoid multivalued cells. Let’s consider an example in the following table.

Here we can see multiple lecturers teaching one subject. Hence, the table has multivalued cells. This contradicts the first normal form. So we have to create separate rows for each multi-valued cell as shown below.

Now we can see the table is in 1NF.
Second Normal Form #
In order to become 2NF, the following conditions need to be satisfied.
- Tables should be in 1 NF ✅
- Relation must not contain any partial dependency ❓
As shown above, the table is already in 1NF. In the above table, all other attributes depend on { Student_Id, Subject_Id, Professor_Id }, which is the composite primary key. But the followings depend on only a part of the composite primary key,
{Student_id} -> {Student Name, City, Region}
{Subject_id} -> {Subject, Credits}
{Professor_id} -> {Professor Name}
These types of dependencies are called Partial Dependencies. However, to achieve 2NF, we need to remove these partial dependencies. Because in 2NF, no non-prime attribute should depend on part of the primary key. All non-prime attributes should depend on the entire primary key.
Following are the tables we get after removing these partial dependencies.
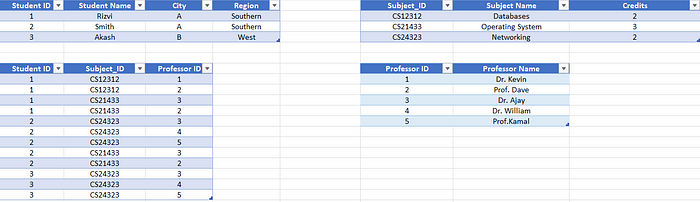
Here we can see that no partial dependencies are remaining. Hence, now it satisfies 2NF.
Third Normal Form #
In order to become 3NF, the following conditions need to be satisfied.
- Tables should be in 1 NF ✅
- Tables should be in 2 NF ✅
- Relation must not contain any transitive dependency ❓
Transitive Dependency occurs when a non-prime attribute depends on another non-prime attribute. The normalization from 2NF to 3NF involves the removal of Transitive Dependencies. Let’s consider our example. In our example, we have the following transitive dependencies.
{City} -> {Region}
We can remove these by placing the attributes in a new relation. Otherwise, there will be update anomalies like,
We need to update Region each time we update City
Here are the tables after removing transitive dependencies.
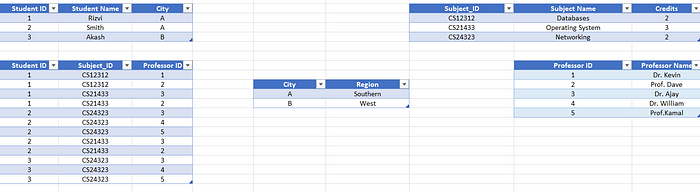
Here we can see, that no transitive dependencies are remaining. So now it satisfies 3NF.
BCNF #
BCNF is the advanced version of 3NF. In order to become BCNF, the following conditions need to be satisfied.
- Tables should be in 1 NF ✅
- Tables should be in 2 NF ✅
- Tables should be in 3 NF ✅
- For every functional dependency X->Y, X is the super key of table❓
As discussed so far, the tables are in 3NF. Now, we can decompose the above tables as follows, in such a way that it satisfies the 4th condition,
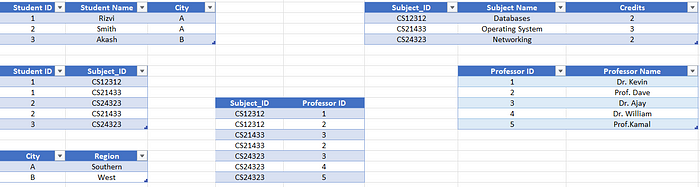
Likewise, we can continue applying more levels of database normalization, such as 4NF and 5NF. However, in this article, we discussed only up to BCNF. By adhering to the principles of normalization, databases can be designed and maintained more efficiently, leading to better overall data management and system performance.
Thank You.
Happy Coding 🙌